Table of Contents
누적합(Prefix Sum)과 부분합
누적합 (Prefix Sum)은 배열의 각 요소에 대해 이전 요소들의 합을 누적해서 저장한 배열이다. 배열의 값들이 변하지 않는다면 누합 또한 변경되지 않는다.
미리 구해둔 누적합을 통해 배열의 특정 구간의 부분합을 빠르게 계산할 수 있다.
1차원 배열 누적합
주어진 배열의 첫 번째 요소부터 마지막 요소까지 순차적으로 탐색하면서 현재 요소까지의 누적합을 계산하여 새로운 배열에 저장한다.
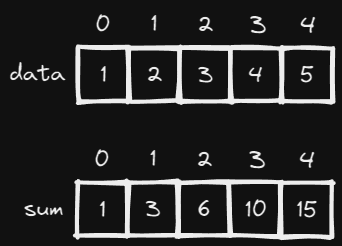
sum[i] 에는 data[0] + data[1] + … data[i - 1]의 값이 들어간다.
즉, sum[i] = sum[i - 1] + data[i] 이다.
코드로 나타내면 다음과 같다.
1def prefix_sum(n):
2 sum = [0]*n # 누적합을 담을 빈 배열 생성
3 sum[0] = data[0] # 첫번째 값 생성
4 for i in range(1,n): # 두번째 값부터 누적합을 저장
5 sum[i] = sum[i-1] + data[i]
6 return sum
7
8n = int(input())
9data = list(map(int, input().split()))
10sum = prefix_sum(n)
시간복잡도는 O(n) 이 된다.
1차원 배열 부분합
누적합을 이용하여 배열의 일부 구간에 대한 합을 빠르게 구할 수 있다.
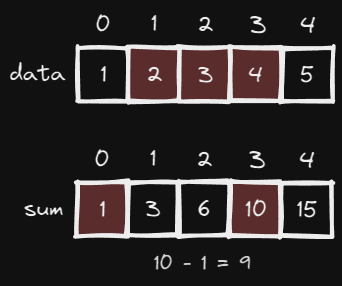
data 배열의 1 ~ 3까지의 부분합을 구하려면 3까지의 누적합에서 1까지의 누적합을 빼면 된다.
즉, data 배열의 i 항 부터 j 항까지의 합을 구할 경우 prefixSum = sum[j] - sum[i -1] 이 된다.
2차원 배열 누적합
2차원 배열은 1차원 배열의 누적합 개념에서 왼쪽에서 오른쪽 방향, 위에서 아래방향 두 번의 쿼리 단계를 거쳐야 한다.
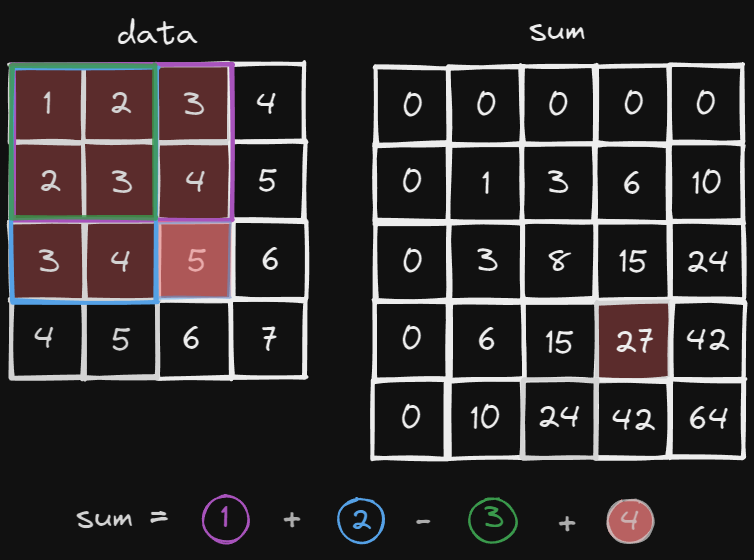
sum[i][j] 에는 data[0][0] 부터 data[i - 1][j - 1] 까지의 합이 담겨져 있다.
즉, sum[i][j] = data[0][0] + data[0][1] + ... + data[0][j-1] + ... + data[i-1][j-1] 이 된다.
이를 다르게 풀면 sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + data[i-1][j-1] 이 된다.
코드로 나타내면 다음과 같다.
1def prefix_sum(n,m):
2 sum = [[0]*(m+1) for _ in range(n+1)]
3 for i in range(1,n+1):
4 for j in range(1,m+1):
5 sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + data[i-1][j-1]
6 return sum
7
8n,m = map(int, input().split())
9data = [list(map(int, input().split())) for _ in range(n)]
10prefixSum = prefix_sum(n,m)
시간복잡도는 O(N**) 이 된다.
2차원 배열 부분합
2차원 배열 또한 누적합을 이용하여 배열의 일부 구간에 대한 합을 빠르게 구할 수 있다.
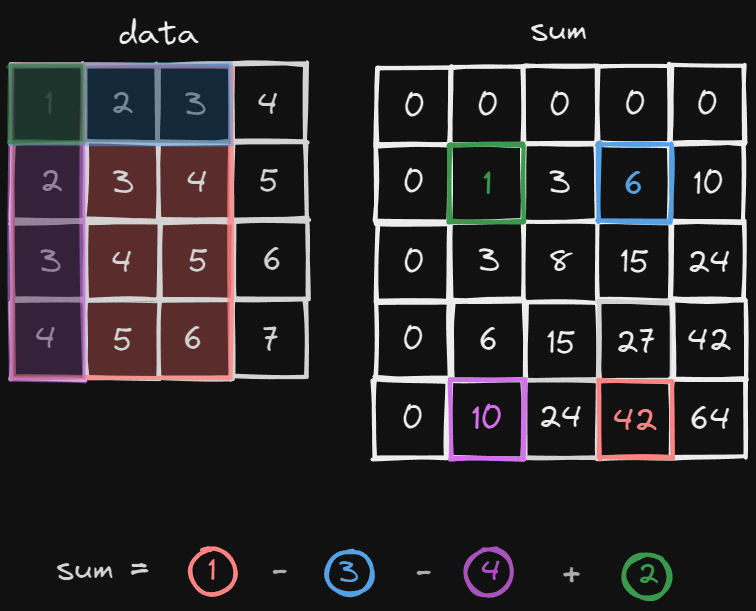
data 의 (x1, y1) 부터 (x2, y2) 까지의 합은 sum[x2+1][y2+1] - sum[x1][y2+1] - sum[x2+1][y1] + sum[x1][y1] 이 된다.